こんにちは。AIチームでデータアナリストを担当している柾屋(まさや)です。アドベントカレンダー5日目の記事になります。
今回はミッションの1つで担当しているA/Bテストの評価方法についての内容です。
AI Shiftではベイズ推定を用いたA/Bテストの評価を行なっています。実際に実務でベイズ推定を利用した評価のアウトプットや評価の解釈で悩んだ点についてまとめていきます。
ベイズ推定とは何か?
正直に申しますと、私はベイズ理論についてそんなに詳しくありません(笑)
ここでは詳細な理論ではなく、ざっくりと「ベイズ推定とはどのようなものなのか?」について簡単に紹介します。
直感的に理解しやすく、参考になったサイトがこちらです。具体的な事例を用いながらベイズ推定の中身を紹介してくれているので、とても分かりやすいです。
このサイトでは、ベイズ推定を「事前に決めておいた確率分布と得られたデータを使って、事象の発生確率を決めること」と定義しています。
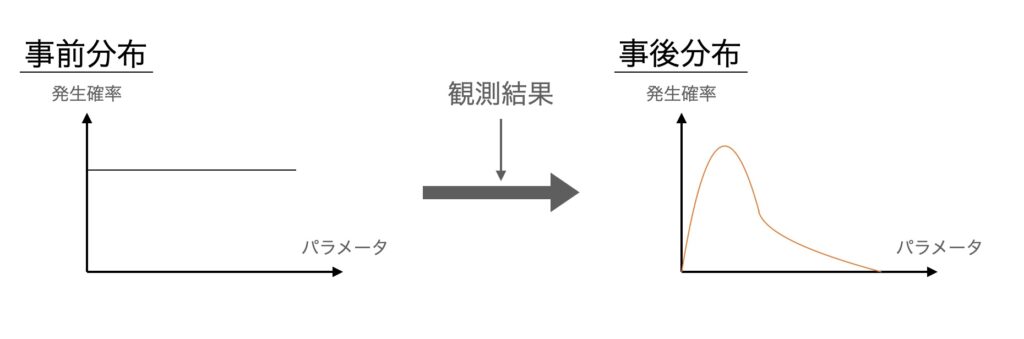
具体的な問題を使ってベイズ推定を理解する
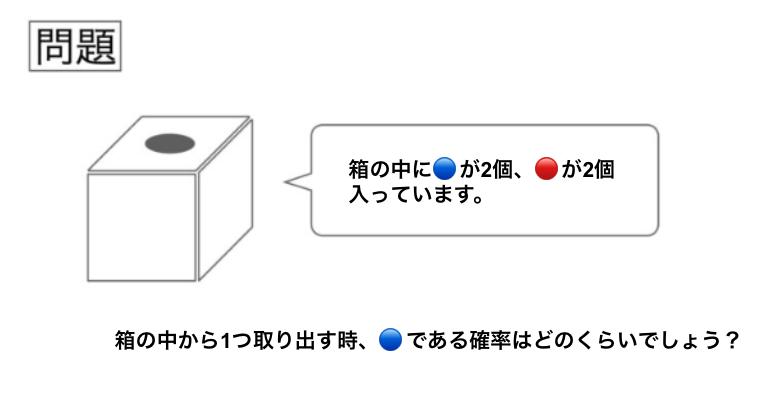
通常の確率問題の場合は、下記のように"箱に入っている青玉、赤玉の個数が決まっており、その上で、青玉である確率はどのくらいか?"という問題設定が多いかと思います。
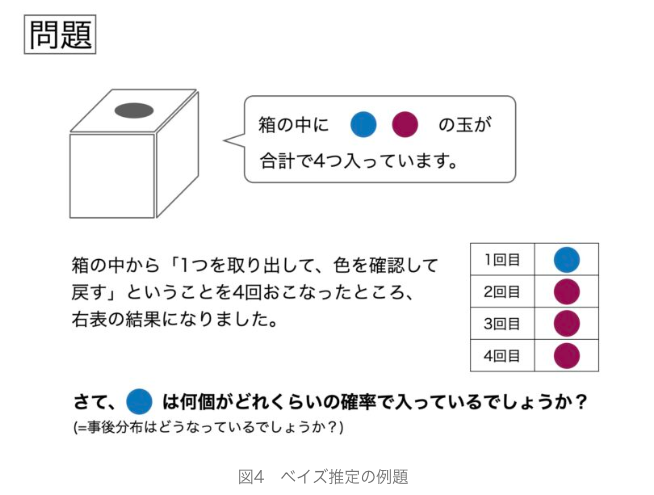
対してベイズ推定の場合は、下記のように"箱に入っている玉の色の種類は分かるが、それぞれの個数が不明の状態で、実際に取り出してみた実績をもとに、青玉が入っている個数の確率を求める"という問題設定になります。
ビジネスの世界においては、前者の問題のように最初から箱の中に入っている母数の内訳が判明していることはありません。
「商品Aを売った時に、誰がどのくらいの確率で買ってくれるのか?」という問題を考えてみると、より直感的に理解しやすいと思います。
最初から商品Aを誰が買うのかが決まっている(=箱の中の赤玉と青玉の数が決まっている)ということは、ゲームなどの決まったシナリオの世界でない限りはありえませんよね。
そのため、ビジネスでの問題では上記の問題のように、商品Aを買う可能性のある人や何人いるのかはおおよそ決まっている(=箱の中に赤色と青色が合計でxx個入っている)が、それ以外は決まっていない(=箱の中に赤色がxx個、青色がxx個かは分からない)という条件下考えるケースの方が圧倒的に多くなります。
定義に照らし合わせて問題を考えてみる
話が少し脱線しましたが、上記の問題をベイズ推定の定義に合わせてみると、下記のように言い換えができます。
ベイズ推定とは、
「事前に決めておいた確率分布と得られたデータを使って、事象の発生確率を決めること」

(定義)事前に決めておいた確率分布
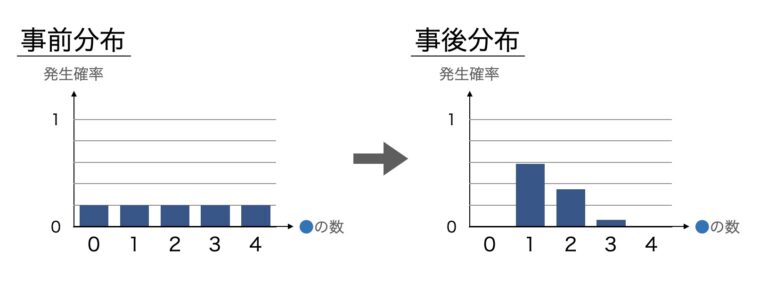
(問題)「観測前の段階では青玉が0個~4個の確率を均等である(1/5)と考える」
→事前分布は1/5の一様分布
(定義)得られたデータを使って
(問題)「1回目に青玉、2,3,4回目に赤玉が出たというデータから、青玉が1個~3個の条件付き確率を出す」
→青玉が1個の場合は 27/ 256 (1/4 × 3/4× 3/4× 3/4)
→青玉が2個の場合は 16/ 256 (2/4 × 2/4× 2/4× 2/4)
→青玉が3個の場合は 3/ 256 (3/4 × 1/4× 1/4× 1/4)
※青玉と赤玉がそれぞれ出ているので青玉が0個、4個のケースはない
(定義)事象の発生確率を決めること
(問題)「事前に決めておいた確率と算出した条件付き確率を掛け合わせて、正規化※1 をした値から事後分布を作成する」
※1: 合計1にする処理
→青玉が0個の確率: 0
→青玉が1個の確率: 27/46
→青玉が2個の確率: 16/46
→青玉が3個の確率: 3/46
→青玉が4個の確率: 0
なんとなくベイズ推定についてイメージがついてきたのではないでしょうか!?
なぜA/Bテストの評価にベイズ推定を用いることにしたのか?
次に、「なぜA/Bテストの評価においてベイズ推定を活用しているのか?」について紹介します。
結論は、「単純な勝ち負け(or 判定できない)という結果ではなく、どの程度の割合でA(or B)が良いのかが分かるため」です。
一般的な信頼区間を用いた仮説検証の場合を考えてみる
※まだ勉強中のため、以下の内容で間違えている箇所があるかもしれませんが、ご容赦ください。。
検証内容:広告Aと広告Bではどちらのクリック率が高いか?
広告Aと広告Bの信頼区間が重なっていない場合は「広告Bの方が広告Aよりクリック率が高く,それらの間には有意な差がある」と判定します。
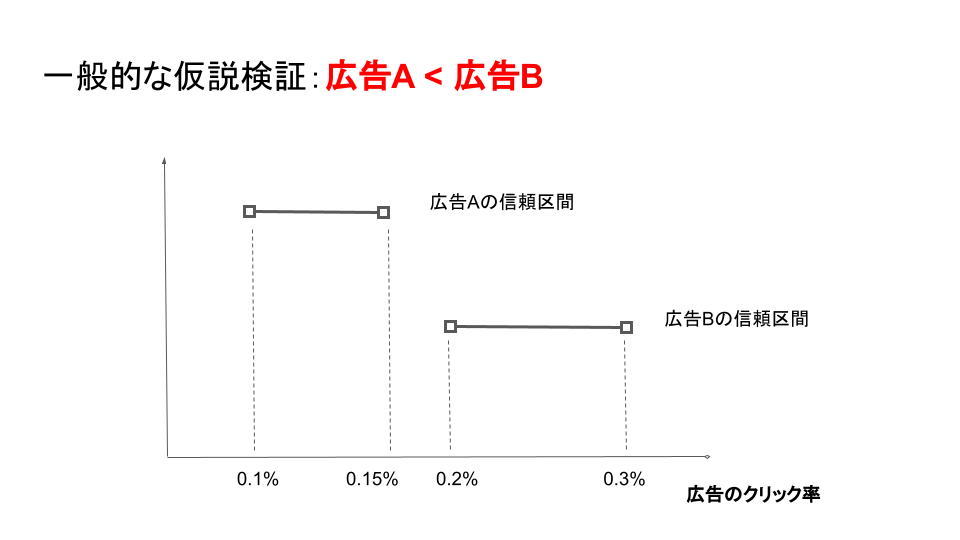
一方で、広告Aと広告Bの信頼区間が重なっている場合、「広告Aと広告Bのクリック率の間には、有意な差はない(誤差の範囲である)」と判定します。
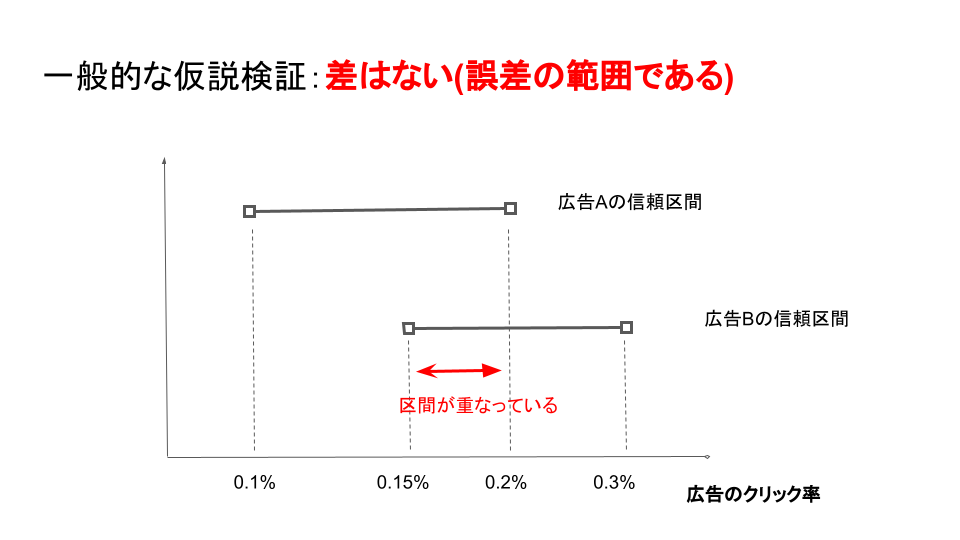
あなたがもし広告の担当者で、どちらかの広告を選択しなければいけない立場だったら困りませんか?もし仮に選択したとしても、その選択に根拠を持たせることは難しいことでしょう。
ベイズ推定を用いた仮説検証の場合を考えてみる
検証内容:広告Aと広告Bではどちらのクリック率が高いか?
ベイズ推定では信頼区間ではなく、広告A、広告Bそれぞれの確率分布を求めます。
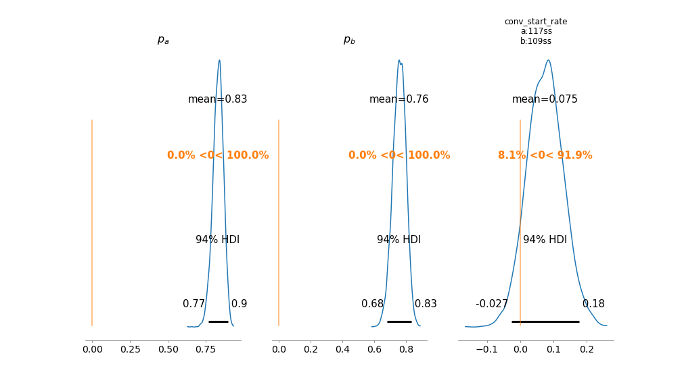
求められた広告Aの確率分布(以下Paとする)から広告Bの確率分布(以下Pbとする)の差分を取ることで、新しく広告Aと広告Bの差分の確率分布(以下Pa-Pbとする)を求めることができます。
Pa-Pbがゼロ(オレンジの線)を基準として正の領域(右側)の割合が大きいのか、負の領域(左側)の割合が大きいのかでPaとPbのどちらの確率分布が大きい値を取る可能性が高いのかを判断することができます。
上記の例では、広告Aのクリック率の方が広告Bのクリック率よりも高い確率が91.9%であると判定することができます。
このように、広告Aと広告Bのクリック率の勝敗だけでなく、”どの程度勝っていたのか?"を確認できるため、A/Bテストの検証においてベイズ推定が活用されています。
実際にテストしてみたA/Bテスト評価結果を紹介
やっと本題です。実際にA/Bテストの評価をベイズ推定を用いて行ってみましたので紹介します。
検証背景
ボイスボットでは一定の割合でどうしても、会話途中で離脱してしまうユーザーが存在しています。このようなユーザーが最後まで会話を続けてくれるためにどのようなチューニングを行えば良いのでしょうか?
チューニングポイントは様々ですが、今回はその中の1つである、"ボイスボットの話すスピード"に着目してA/Bテストを実施しました。
実施した業界・ボイスボットの活用方法
- 業界:B2Cのインターネットサービス
- 活用方法:利用ユーザーからの問合せでボイスボットを利用
A/Bテストの設定
- A:ボイスボットの話すスピードをゆっくりにする(確率分布をPaとする)
- B:ボイスボットの話すスピードを早めにする(確率分布をPbとする)
評価のポイント
- 指標1: ボイスボットと会話を開始した割合(以下、会話開始率)
- 指標2: ボイスボットと会話をして最後まで完遂した割合(以下、完遂率)
A/Bテスト実施前の仮説
問合せを行ったユーザーの多くが40-60代であった為、ゆっくり話す方が最後まで完遂してくれる割合が高いのではないかと仮説立てをしました。
A/Bテストの結果
結論
ボイスボットの話すスピードが早い方がゆっくりな方よりも指標1(会話開始率)のスコアが高い確率が99.6%、指標2(完遂率)のスコアが高い確率が89.4%でした。
指標1(会話開始率)の評価の詳細
Pa(ゆっくり話す)の確率分布
・平均: 91.8%
・3%HDI地点: 89.9%
・97%HDI地点: 93.7%
・97%HDIの幅(97%HDI地点 - 3%HDI地点): 3.8%
Pb(早く話す)の確率分布
・平均: 95.2%
・3%HDI地点: 93.9%
・97%HDI地点:96.5%
・97%HDIの幅(97%HDI地点 - 3%HDI地点): 2.6%
Pa - Pb
Pa - Pbの正の割合: 99.6%
指標2(完遂率)の評価の詳細
Pa(ゆっくり話す)の確率分布
・平均: 88.4%
・3%HDI: 86.0%
・97%HDI:90.7%
・97%HDIの幅(97%HDI地点 - 3%HDI地点): 4.7%
Pb(早く話す)の確率分布
・平均: 90.5%
・3%HDI: 88.4%
・97%HDI:92.7%
・97%HDIの幅(97%HDI地点 - 3%HDI地点): 4.3%
Pa - Pb
Pa - Pbの正の割合: 89.4%
ベイズ推定の評価について悩んだポイント
ここからは、ベイズ推定を用いた評価を行った際に悩んだポイントについて記載します。
1. 事前分布と事後分布でどのような分布を活用すれば良いのか?
ベイズ推定では、事前分布と事後分布を評価者自身で設定しなければいけません。
文系数学で少し触った程度の統計知識では、なかなか事前分布と事後分布で何を設定すれば良いかという感覚が掴めず、苦労しました(笑)
下記が社内で数学スペシャリストにレクチャーしてもらった考え方の順序です。
a.評価したい指標の取りうる値に近しい事後分布を選ぶ
例) ボイスボットの会話開始率(ボイスボットと会話を開始したかどうか)を評価したい場合は取りうる値が0, 1の離散的なデータになる。
→ベルヌーイ分布が良さそうなど
b.事後分布として選択した確率分布に必要なパラメータを決めるための事前分布を選択する
例) ボイスボットでの認識エラー数を評価したい際に事後分布としてポアソン分布を利用する場合、パラメータとしてmuを与える必要があります。
muが取りうる値は[mu >= 0]と定義されています。また、大抵のユーザーはそんなに認識エラーは発生しないため、0付近での値が取りやすい分布になる。
→事前分布としてはガンマ分布が良さそうなど
評価したい指標をグルーピング(平均化する等)してから評価したいなどの場合は、データの形式が離散的から連続的に変わるため、注意が必要です。
私は最初は知識不足で、連続的なデータの場合も、離散的なデータに対応するベイズ推定モデルを使ってしまっていたため、結果がおかしなことになるということが何度かありました(笑)
2.どの程度のデータ量を判断基準とすれば良いのか?
次に集めるべきデータ量についてです。
株式会社AI Shiftでは、dailyでデータが更新されていくため、基本は毎日ベイズ推定を用いて評価を行なっています。
データが集まれば集まるほど、評価のブレが少なくなるのですが、どの程度集めれば良いのかという指標がありませんでした。
十分だと思っていたデータ量でも、データがさらに集まったタイミングで評価が逆転することがあったりするためです。
一般的にはデータは多ければ多いほど良いという見解だと思うのですが、今のところ、97%HDI(事後分布での取り得る値の区間)の幅が10%以下、理想は5%以下としています。
例) 97%HDIの幅が3%の確率分布
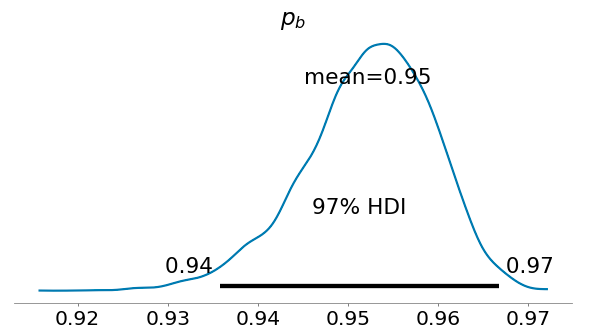
理由は、これまでのA/Bテストの評価データから、10%以上の場合は評価の逆転が起きる可能性は大きく、5%以下の場合はほとんどないという結果だったためです。
他にも参考がないか今後調べて評価の基準値をより精緻にしていきたいと思います。
3.複数の評価指標がある場合での総合判断
複数の指標を評価する場合、一方の評価ではAが勝っているが、もう一方の指標ではBが勝っているということが起こり得ます。
この場合、最初に評価する指標の優先度を決めておかなければ主観的な評価につながる可能性があります。
どうしてもA/Bテストを実施する際に、仮説立てた理論に近づけようという意識が心の片隅に残ってしまうため、主観的な評価を排除するためにも、関係各所と評価についてすり合わせを実施しておくことが肝心だと実感しました。
まとめ
今回はベイズ推定を用いたA/Bテストの評価についてまとめました。
私自身、統計のスペシャリストではないため、日々、模索しながら活用を進めています。この機会に統計について知識を深めつつ、正しい評価のための基準を整えていければと考えています。
最後までお読みいただきありがとうございました。
明日は開発チームの高野よりPMMについての記事が上がります。






