はじめに
こんにちは,AI Shiftの下山です.
この記事はAI Shift Advent Calender 2023の22日目の記事です.
私は最近,効果検証周り,特に弊社プロダクトの1つである自動音声応答サービス AI Messenger Voicebot における効果検証を用いたユーザビリティの向上を担当しています.
Voicebotには,話す速さやピッチ,シナリオ内の文言など,調整可能な変数が多岐に渡り存在しており,効果検証を用いて各変数の最良な値を探索しています.
しかし,複雑な内容の返答が多いドメインでは話速はゆっくりめ,単純な内容の返答が多いドメインでは話速は少し早くても問題ないなど,最良な値は顧客毎に異なると考えられるため,検証に使用できるサンプル(=利用ユーザ or 入電)のセグメントは顧客毎になります.
そのため,サンプルサイズがそこまで大きく確保できないという特徴があります.
そこで,「サンプルサイズが小さい設定でも,"妥当な"効果検証を行うにはどうすれば良いか?」という問いを立て,この問いへの回答を作るためのサーベイを始めました.
私は,"妥当な"の意味を以下の2つのエラー率を適切に制御できることとして定義しています:
- 本来は差がないのに差があると判断される割合
- 本来は差があるのに差がないと判断される割合
1のタイプのエラー率は統計の文脈では type-1 エラー率と呼ばれものに含まれます.
本ブログでは,上述の問いに関係しそうと思われる以下の論文について紹介します:
Small sample sizes: A big data problem in high-dimensional data analysis
この論文では,「小サンプル」と「検証したい指標が複数」という2つの問題にアプローチしています.
私の興味は上述したように主に「小サンプル」ですが,Voicebotではユーザビリティを評価する指標として「ユーザが嫌にならず最後まで電話を続けてくれるか?」「ユーザの音声を正しく認識でき,聞き返しの回数が少ないか?」などそれほど多くは無いですが複数の指標があります.
これらを同時に検証することにおいても,この論文は参考になりそうだと考えています.
本ブログは概要を紹介することに重きを置いて執筆しようと考えていますので,詳細は上記論文に任せようと思います.
統計は勉強し始めでよく分かっていない点も多いため,明るい方がおりましたらアドバイスを頂けますと幸いです.
問題設定
論文では, 1つのサンプルから複数の指標が得られる問題を対象とし,各指標に対する群間差を検定する手法を提案しています.
例として,2つのタイプ(群)のマウスが存在し,マウスの脳内で発生するタンパク質量が群毎に差があるかを評価する問題を考えます.
ここで,指標は計測する脳の領域 6個 \(\times\) タンパク質の種類 6種類 = 36個あるとします:つまり,マウス1匹に対し,\(D=\) 36種類の評価値(=指標の観測値)を得ることができます.
群 i = 1, 2 に対する \(d\) 番目の指標の真の平均を \( \mu_{i, d} \) と書くことにします.
このとき,「タイプの違いが,脳の領域とタンパク質の組み合わせに影響を与えるか?」を検証する問題は,\(d\) = 1, ..., \(D\) それぞれの指標に対する null-hypothesis \( \mu_{1d} = \mu_{2d}\) を検証する問題と考えることができます.
上記のように複数の指標に対する検定として,max t-testと呼ばれる方法があるそうです.
\(d\) 番目の指標に対するt-検定量を \( T_d \) とし,その最大値 \(T_0 := \max \textbf{T}, \textbf{T} := \{T_1, \ldots, T_D\} \) を考えます.
もし,\(T_0\) の従う分布が明に分かれば,その \(1-\alpha\) パーセンタイル \(z_{\alpha}\) を用いて,各 \(d\) 毎に \(|T_d| \geq z_{\alpha}\) なら null-hypothesis を棄却します.
しかし,その分布を明に得ることは難しいです.
\(\textbf{T}\) の従う分布は,漸近的に,平均0でとある共分散行列を持つ多変量正規分布に従いますが,共分散行列は未知の行列に依存しています.
既存手法
上述の「\(\textbf{T}\) が従う分布の共分散行列を明に求められない」という問題に対し,先行研究では,共分散行列を経験共分散行列で置き換える方法が提案されています.
各群のサンプルサイズを \(n_i\) とします.
群 i のマウス \(k \in\) {1, ..., \(n_i\)} から得られた \(d\)番目の指標の観測値を \(Y_{ik, d}\) と書く事にし,これを評価値サンプルと呼ぶ事にします.
経験共分散行列は評価値サンプルを用いて具体的に計算することができるため,これを共分散行列としてもつ平均0の多変量正規分布 \(N_{emp}\) からはサンプルを得ることができます.
この \(N_{emp}\) を 本来知りたい \(\textbf{T}\) の分布の何らかの近似であるとみなし,\(N_{emp}\) からのt-検定量の組のサンプル \(\{\textbf{T}_{emp, i}\}_{i=1}^M\) から求めた \(1-\alpha\) パーセンタイルを本来の \(z_{\alpha}\) の変わりに使用します.
しかしながら,この論文で行ったシミュレーションによると,サンプルサイズ \(n_i\) が小さい(特に10以下の)場合,上記既存手法では type-1 エラー率が10%以上になるケースが報告されています.
ここで,シミュレーションでは真の分布として (i)多変量正規分布 (ii) 多変量t-分布 をそれぞれ用いています.
※ サンプルサイズは,経験共分散の計算に影響することに注意してください.
提案手法
(明確な理由を僕が理解できなかったのですが)
この論文では,既存手法が小サンプルサイズで上手くいっていない要因の1つは \(\textbf{T}\) の分布のパラメータを推定することであるとし,パラメータ推定を行わず\(\textbf{T}\) の従う分布を漸近的に近似する,bootstrapベースの手法を提案しています.
手順は以下です:
- 評価値ベクトルを \(Y_{ik} = (Y_{ik, 1}, Y_{ik, 2}, \ldots, Y_{ik, D})\) と書くことにし,これを中心化した変数 \(Z_{ik} = Y_{ik} - \frac{1}{n_i} \sum_{k=1}^{n_i} Y_{ik} \) を考えます.
- この変数に,ランダム符号 \(W_{ik} \sim P(W_{ik} = \pm 1) = 1/2 \) をかけた変数 \(Z^\ast_{ik} = W_{ik} Z_{ik}\) を作ります.
- この変数 \(\{Z^\ast_{ik}\}_{i=1,2, k=1, 2, \ldots, n_i}\) から t-検定量の組 \( \textbf{T}^\ast := (T^\ast_1, \ldots, T^\ast_D) \) を作成し,\(T^\ast_0 := \max \textbf{T}^\ast \) を得ます.
- step 2 と 3 を \(M\) 回繰り返して得られるサンプル \(\{T^\ast_{0, j}\}_{j=1}^M \) による経験分布の \(1-\alpha\) パーセンタイルを \(Z^\ast_{\alpha}\) とし,これを \(Z_{\alpha}\) の変わりに使用します.
論文曰く,\(\textbf{T}^\ast\) の分布は本来知りたい \(\textbf{T}\) の分布を理論的に近似できているようです.
補足資料に証明が載っているそうなのですが,まだ読めていません.
検証と結果
論文では,既存手法と比較して,提案手法が type-1 エラー率を 適切に制御できていることを示すために,真の分布を仮定したシミュレーションにより性能を評価しています.
真の分布として,歪んだ分布 3 種類(\(\chi_7^2\), \(\chi_{15}^2\) , exponential)および 対称的な分布 3 種類(normal, logistic, \(T_3\) )を使い,それぞれに対し,検定する評価値の個数 \(D\) とサンプルサイズ \(n_i\) をいくつか変えてシミュレーションを行なっています.
このとき,type-1 エラー率が5%以下であれば適切に制御できている,5%を超えると適切に制御できていないと判断します.
以下に論文から引用した結果の図を記載します.
Wild が提案手法,Chang が既存手法,\(q\) がこのブログの \(D\) に対応します.また,縦軸が type-1 エラー率です.
シミュレーション結果では,そのどの組み合わせにおいても,既存手法は type-1 エラー率が 5% より上回る一方で,提案手法は type-1 エラー率が 5% 以下か同程度に抑えられています.
個人的に興味深いのは,興味を持っている設定と近い状況である「検証したい指標が少ないとき,つまり \(q\) が小さいとき」においても,提案手法は type-1 エラー率を適切に制御できている一方で,既存手法は失敗している点です.
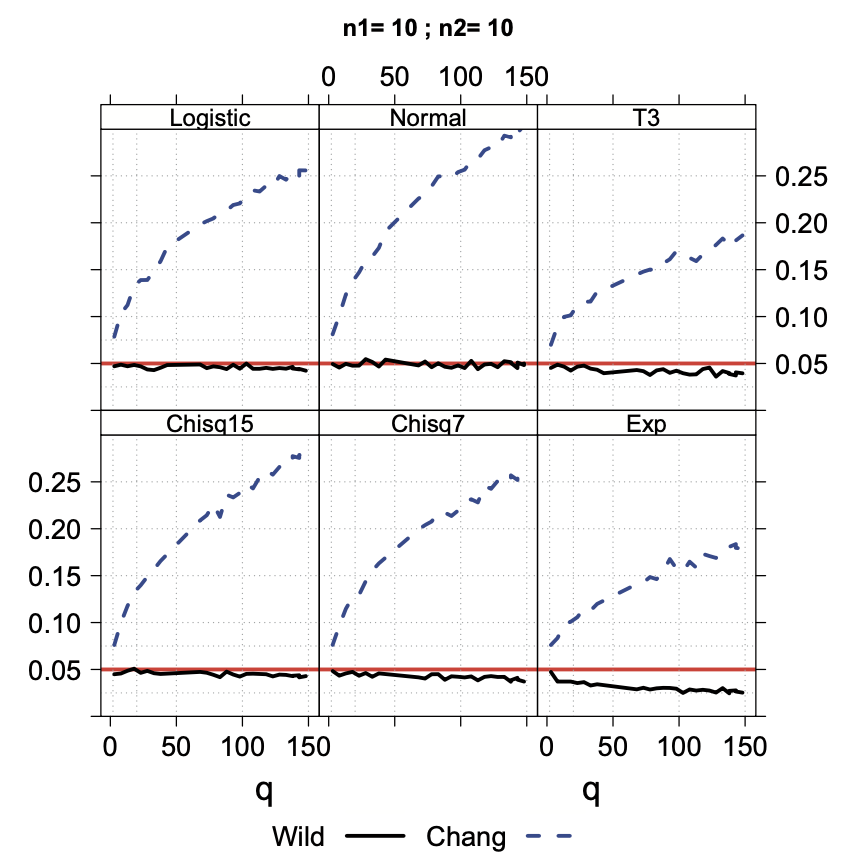
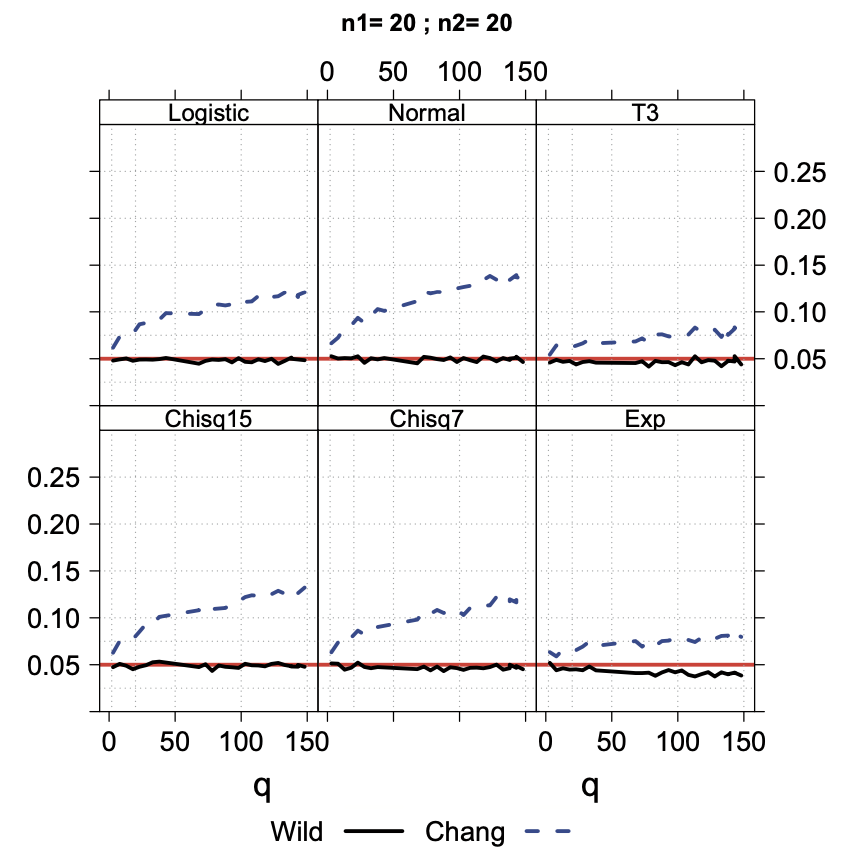
(論文より引用)
終わりに
本ブログでは,小サンプルサイズにおいて複数指標の検定を行う際に type-1 エラー率を適切に制御する事に注目した論文の1つを紹介しました.
null-hypothesis が従う分布のパラメータを推定しない,ランダム符号を用いた resampling ベースの手法が提案されました.
シミュレーションベースの実験から,パラメータ推定を行う既存手法が適切に type-1 エラー率を制御できないケースにおいても,提案手法は適切に制御できることが報告されました.
統計は全く詳しくないので,この論文を通じて学べることが多くありとても勉強になりました.
しかし,自分の中でまだ以下の点について理解できていません:
- 複数指標を検定する際に使われる max t-test の基礎理論;
- 提案された resampling ベースの方法により得られる確率変数の分布が漸近的に null-hypothesis の分布に一致する理論的保証;
- 小サンプルサイズの設定において,パラメータ推定を行う既存手法が type-1 エラー率を適切に制御できない理論的説明.
ですので,引き続き勉強を行いこれらの点をはっきりと理解したいです.
ここまで読んでくださいましてありがとうございました!
AI Shiftではエンジニアの採用に力を入れています! 少しでも興味を持っていただけましたら,カジュアル面談でお話しませんか? (オンライン・19時以降の面談も可能です!) 【面談フォームはこちら】






