はじめに
こんにちは,AIチームの下山です.
弊社では自動音声対話サービスVoicebotにおける施策の検証方法として,ベイジアンA/Bテストを採用しています.
(ベイジアンA/Bの概要についてはこちらの記事をご覧ください).
本記事では,ベイジアンA/Bにおいて,効果が高い施策の選択を間違える(例えば,AとBの比較を行い,本来はAの方がBより効果が高いのにBを選択してしまう)可能性をある程度抑えるために必要なサンプルサイズの見積もり方について,ヒューリスティックな方法を構築しましたのでそれについて紹介します.
(私の調査不足かもしれませんが)ベイジアンA/Bにおけるサンプルサイズの見積もり方に関して扱っている日本語の記事はそれほど多くあるわけではないと思っており,この記事がこのトピックへの情報提供の一助になれば幸いです.
モチベーションと背景
私たちはVoicebotでのユーザ体験に影響を与える変数(例えば,話速,シナリオ内容など)の最良値の探索にベイジアンA/Bテストを活用しています.
ここでは,例として,VoicebotにおけるシナリオとしてAパターン・Bパターンを用意し,離脱率が低い方が良いという観点のもと,どちらのシナリオが良いか?の検証を考えます.
また,AパターンBパターンどちらが良いのか?断定を保留にするのか?の判定は事後分布を用いて計算した確率に基づいて定量的に行うとします.
A/Bテストの検証期間内に得られるデータは有限であるため,本来はAパターンよりBパターンの方が良かったとしても,データの偏りなどにより次のように判定してしまう場合が存在します:
- Aの方が良いと判定
- Aが良いかBが良いか断定できない(保留)
実際,プロダクトで検証を行なっていると,同じ内容のA/Bテストを複数回行った際に,1回目では「Aの方が良い」と判定されたが2回目では「Bの方が良い」と判定されるように,何回目のテストかによって判定結果が変わってしまう事象が観測されました.
つまり,そのようなA/Bテストでは,AとBのどちらが良いかの判断を間違えてしまっている可能性があります.
特に,このような事象はサンプルサイズが小さい時に発生しやすいことも分かっています.
本来はBの方が良いときに,判定1が起こってしまう確率を誤り率,判定2が起こってしまう確率を保留率と呼ぶことにすると,上述した問題に対処するために誤り率と保留率を十分抑えるサンプルサイズが知りたいというモチベーションが生まれます.
実は,A/Bテストに頻度論的な統計的仮説検定を用いた場合には,少なくとも誤り率を抑えるために必要なサンプルサイズを計算することができます.
しかし,ベイジアンA/Bにおいては厳密な計算方法が現状は無いと思われます(私の勉強不足な可能性もありますので,ご存じの方がいましたらぜひ教えていただきたいです).
そこで,本記事では,論文「Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors」の内容を参考に,実行予定のベイジアンA/Bにおいて,誤り率と保留率を抑えるために必要なサンプルサイズを見積もるためのヒューリスティックな方法を構築します.
見積もり方法とシミュレーション結果
上述の論文では,2施策の比較の統計的検定に対し,誤った施策を選択してしまう確率を検証後に見積もる方法が提案されています.
この方法のキーアイデアは「シミュレーションにより同一内容の検証を複数回行うことで,そのデータを用いて検定方法が誤った施策を選択してしまう確率を評価する」です.
このアイデアを活用します.
先ほどの例,シナリオAとBの比較,を考えます.
ここでは,比較したい指標が離脱率,1通話に対し得られるデータが離脱したか否かの2値ですので,事前分布をベータ分布,事後分布をベルヌーイ分布とします.
シナリオAに対する事後分布とシナリオBに対する事後分布の差を判定分布\(P_{A-B}\)と呼ぶことにすると,この判定分布を用いてAとBどちらが良いかを以下のように判定することにします:
- Aの離脱率がBの離脱率以下になる確率が \(T_{judge}\) 以上,つまり \(P_{A-B}(\{\leq 0 \}) \geq T_{judge} \),ならAの方がBより良いと判断
- Bの離脱率がAの離脱率以下になる確率が \(T_{judge}\) 以上,つまり \(P_{A-B}(\{\geq 0 \}) \geq T_{judge} \),ならBの方がAより良いと判断
- それ以外の場合,AとBどちらが良いかは保留
では,本当はBの方がAより良いと仮定した際,このベイジアンA/Bにおいて誤り率と保留率を抑えるために必要なサンプルサイズはいくつでしょうか.
先の論文のアイデアを活用し,サンプルサイズを見積もるシミュレーションに基づいた方法を以下のように構築します:
- 入力:Aの離脱率 \(\theta_A\), シナリオAに対する離脱率とシナリオBに対する離脱率の差 \(d\), サンプルサイズ \(N\)
- \(T\) 回繰り返す
- 確率 \(\theta_A\) のベルヌーイ分布から \(N\) サンプル \(D_A\) をサンプリング,確率 \(\theta_A - d\) のベルヌーイ分布から \(N\) サンプル \(D_B\) をサンプリング
- \(D_A\) と \(D_B\) を用いて作成した判定分布 \(P_{A-B}\) に基づいて,"Bが良い","Aが良い","保留"のいずれかを上述した判定ルールに基づき決定
- T回中,"Aが良い"の割合・"保留”の割合を計算し,これらをそれぞれ誤り率・保留率とする
この方法は,Aに対するデータの真の分布とBに対するデータの真の分布を仮定した仮想環境下において,同じ内容のベイジアンA/Bを何回も行うことで,誤り率と保留率を計測しています.
そして,この仮想環境下でのベイジアンA/Bの誤り率と保留率が本番環境下(今回の例では,実際にVoicebotでシナリオAとシナリオBをテストすること)における誤り率と保留率を表しているだろうと考えます.
※ この考えは理論に基づいている訳ではなく,直感的にしたがっています.その意味で,"ヒューリスティックな方法"と述べています.
ここまでの内容のコードは以下です:
ここで,イテレーション回数は \(T=500\) としています.
import numpy as np
from scipy.stats import beta as scipy_beta
def decision_rule(samples_diff, t_judge):
a_leq_b_prob = np.count_nonzero(samples_diff <= 0) / len(samples_diff)
b_leq_a_prob = np.count_nonzero(samples_diff >= 0) / len(samples_diff)
if a_leq_b_prob >= t_judge:
return 'A'
elif b_leq_a_prob >= t_judge:
return 'B'
else:
return 'nothing'
def ABtesting(p_true_A, p_true_B, n_sample, t_judge):
D_A = np.random.binomial(1, p_true_A, size=n_sample)
D_B = np.random.binomial(1, p_true_B, size=n_sample)
# A群に対する事後分布
S_A = D_A.sum()
N_A = len(D_A)
samples_A = scipy_beta.rvs(2 + S_A, 2 + N_A - S_A, size=(2, 30000))
# B群に対する事後分布
S_B = D_B.sum()
N_B = len(D_B)
samples_B = scipy_beta.rvs(2 + S_B, 2 + N_B - S_B, size=(2, 30000))
diff_samples = (samples_A - samples_B).flatten()
win_treatment = decision_rule(diff_samples, t_judge)
return win_treatment
def type_error_estimates(p_true_A, true_diff, n_sample, t_judge):
p_true_B = p_true_A - true_diff
n_iters = 500
error_count = 0
no_win_count = 0
for _ in range(n_iters):
win_treatment = ABtesting(p_true_A, p_true_B, n_sample=n_sample, t_judge=t_judge)
if win_treatment == 'A':
error_count += 1
elif win_treatment == 'nothing':
no_win_count += 1
return error_count/n_iters, no_win_count/n_itersでは,上の方法に基づいて,誤り率と保留率を抑制するために必要なサンプルサイズを見積もってみます.
Aの離脱率 \(\theta_A\) はこれまでの入電記録の平均を取ることにし,それを仮に \(0.1\) だとします.AとBの差は期待される差を設定することにし,仮に \(d=0.03\) とします.
また,AとBそれぞれの離脱率に差があると判断するための閾値である \(T_{judge}\) の値を仮に \(T_{judge} = 0.8\) とします.
サンプルサイズを \(N = 10, 30, 50, 70, 100, 300, 500, 1000, 2000\) と変化させた時のエラー率と判断保留率を評価します.
np.random.seed(42)
n_samples = [10, 30, 50, 70, 100, 300, 500, 1000, 2000]
error_rates, no_win_rates = [], []
for _ in range(5):
error_rates_tmp, no_win_rates_tmp = [], []
for n in n_samples:
error_rate, no_win_rate = type_error_estimates(p_true_A=0.1, true_diff=0.03, n_sample=n, t_judge=0.8)
error_rates_tmp.append(error_rate)
no_win_rates_tmp.append(no_win_rate)
error_rates.append(error_rates_tmp)
no_win_rates.append(no_win_rates_tmp)import matplotlib.pyplot as plt
#plot figure
plt.clf()
fig, axes = plt.subplots(1, 2, figsize=(24, 8))
axes[0].plot(n_samples, np.mean(error_rates, axis=0))
axes[0].scatter(n_samples, np.mean(error_rates, axis=0))
axes[0].set_xscale('log')
axes[0].set_title('Error rates', fontsize=20)
axes[0].tick_params(labelsize=18)
axes[1].plot(n_samples, np.mean(no_win_rates, axis=0))
axes[1].scatter(n_samples, np.mean(no_win_rates, axis=0))
axes[1].set_xscale('log')
axes[1].set_title('No win rates', fontsize=20)
axes[1].tick_params(labelsize=18)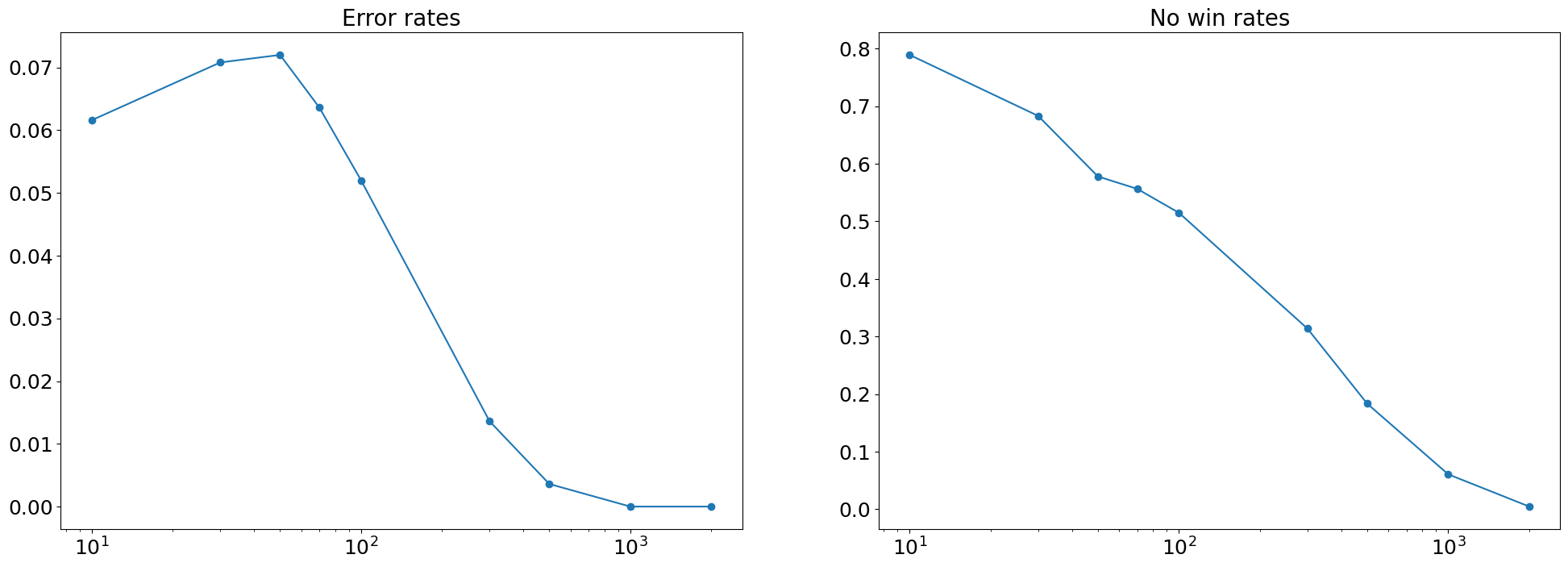
サンプルサイズに対する,誤り率と保留率の推移は上図のようになりました.
この結果を見ると,今回のベイジアンA/Bの設定では,誤り率を5%程度に抑えたい場合,サンプル数を100以上は用意する必要がありそうだということが分かります.
しかし,サンプルサイズ100程度だと,保留率が50%程度あり半分以上の割合で意思決定が保留されることになりそうだということもわかります.
そして,保留率を10%以下に抑えたいとすると,サンプルサイズは1000以上は必要そうです.
終わり
本記事では,ベイジアンA/Bにおいて,誤った施策を選んでしまう確率・どの施策も選ばないと判断を保留する確率,これら2つの確率の抑制に必要なサンプルサイズを見積もるシミュレーションベースの方法を構築しました.
ただ本記事の方法は理論的背景ではなく「同じ内容のA/Bテストを仮想的に何回も繰り返すことで,与えられたサンプルサイズに対して上記2つの確率を見積もる」という考え方に基づいたヒューリスティックな方法でした.
今回の記事がベイジアンA/Bにおけるサンプルサイズの決め方の参考の1つとなれば幸いです.






